Infragravity Waves
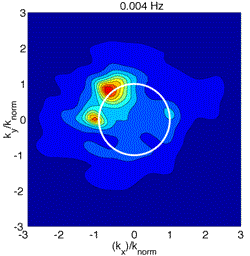
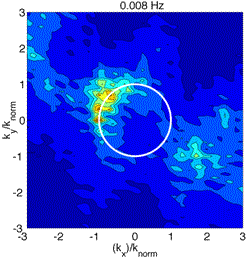
Beamforming of Infragravity waves using an array of pressure gauges on the deep ocean floor (see Webb et al. [1991]). Hot colors indicate where the wave energy is focussed in wavenumber space. The white circle is the predicted wavenumber for linear ocean surface gravity waves
Infragravity waves are low frequency ocean surface gravity waves that are generated by non-linear interactions between ocean surface wind waves. At the sea surface, they are invisibly small (only a few millimeters or centimeters tall over several hundreds of meters to tens of kilometers long), but they contribute significantly to the seafloor pressure signal because they are much less attenuated with depth than the much shorter wavelength wind waves. Infragravity waves are generated as forced waves with a complicated frequency-wavenumber relation, but they are converted to free (linear) waves through shoaling processes at coastlines. Linear ocean surface gravity waves have the dispersion relation:
which gives a wavelength of XX in shallow water and of XX in deep water. Most of the energy is at wavelengths much longer than the water depth, so the waves are refractively steered back to coastlines, but a little bit of it escapes and can cross oceans unattenuated (Webb et al., 1991). The free waves are generally longer than the forced waves, so they decay less with depth, and the seafloor infragravity wave signal comes almost entirely from free waves at depths greater than 100 m (Okihiro et al., 19XX). Figure 1 shows the wavenumber spectrum of infragravity waves measured at the deep seafloor, which clearly fall on the free surface wave velocities.
The seafloor pressure spectrum is very different from that at the sea surface, because of the strong filtering out of all energy with wavelengths shorter than the ocean depth. When two wind waves interact, the second-order non-linear terms have frequencies and wavenumbers equal to the sum and the differences of those of the interacting waves. When the wavenumbers are subtracted from one another, a very long wavelength wave can be created. Since the pressure from surface waves decays exponentially at a rate equal to the wavelength, only long wavelength waves contribute significant energy to They have a simple dispersion relation, allowing us to calculate their wavelength as a function of ocean depth, which is indispensable for calculating compliance. The dispersion relation is:
This is the same dispersion relation that governs wind waves and tsunamis. Infragravity waves that are detectable at the seafloor are longer than the ocean depth, so their velocity is approximately the square root of the water depth times the gravitational acceleration (~10) have velocities comparable to those for tsunamis
Normal wind waves dominate at the sea surface, but infragravity waves dominate at seafloor depths greater than 100 m. This is because the surface wave energy decays exponentially with depth, with the rate of decay equal to the surface wavelength. Most wind wave energy is at wavelengths less than 100 m, so little of this energy reaches the deep seafloor. Infragravity waves can have much longer wavelengths and so the portion of the infragravity waves with wavelengths longer than the water depth can generate a detectable seafloor signal.
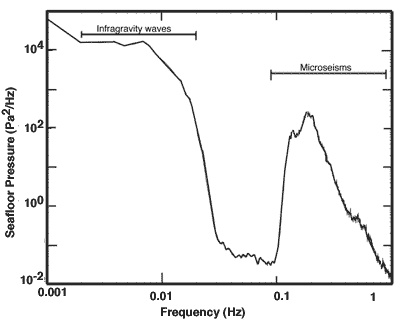
Figure 2: Typical deep seafloor pressure spectrum (from a site in 2.2 km water depth).
Figure 2 shows a typical seafloor pressure spectrum. The infragravity waves create the signal below 0.02 Hz. The high-frequency cutoff depends on the water depth, increasing in frequency for shallower water depths. This cutoff corresponds to the frequency at which the wavelengths are equal to
Beamforming of low frequency pressure energy recorded by a seafloor pressure sensor array shows that the source of this energy falls on the linear ocean surface gravity wave curve (Figure 2).
Infragravity waves are created by non-linear interactions between ocean surface wind waves that are traveling in different directions [Webb et al., 1991]. The pressure signal from ocean surface waves decays exponentially with depth as a function of their wavelength. Infragravity waves are much smaller than normal wind waves at the sea surface, but they are also much longer. In deep water, therefore, all of the normal wind wave energy is filtered out and only the infragravity wave and microseism signals make it to the seafloor (Figure 1).
We don't use the microseisms because they are a mix of seismic interface waves and complicated locally excited waves. The seismic interface waves aren't interesting for compliance because their pressure-displacement transfer function is only sensitive to the water density [Webb, 1998] and we can't calculate the wavenumber for the locally excited waves.
We measure compliance at such low frequencies because there is no useable signal at higher frequencies. In deep water, the pressure signal comes from linear surface gravity waves at low frequencies and from non-linear wave-wave interactions at higher frequencies. Ocean surface waves are strongest at 5 to 15 seconds period [Pierson and Moskowitz, 1964], but almost none of this energy makes it to the deep seafloor because the pressure decays exponentially with depth so that, at one wavelength depth, the pressure signal is 500 times smaller than at the surface, and at two wavelengths depth the pressure is nearly 300,000 times smaller. Therefore, only waves with wavelengths longer than the ocean depth usually create a detectable seafloor signal. These are the "infragravity" waves that we use.
There is also a higher frequency seafloor pressure signal, known as the "microseism" band, but their wavelength is too unpredictable to use. The microseism signal is a mix of local nonlinear surface gravity waves and seismic interface waves. The seismic waves are excited by local nonlinear surface gravity waves when these waves are very strong, for example underneath storms. To calculate compliance, we need to know the wavelength of the source waves, but the nonlinear surface waves have no predictable frequency-wavenumber relation and the seismic interface waves change modes and therefore wavelengths over short distances.
There is no good signal at shorter periods because short-period pressure energy is strongly filtered with depth. The shallower the water, the more short-period energy we will be able to measure. In deeper water, the frequency band is smaller but, because the surface waves are longer, we can detect features that are deeper in the subsurface.
To determine the subsurface structure from compliance data, we have to know the wavelength of the forcing waves. so we calculate compliance at frequencies where the pressure comes from linear ocean surface gravity waves. The energy from these waves only reaches the seafloor if their wavelength is longer than the ocean depth, limiting the frequency band of compliance measurements. In generaly, if the water is deeper than 0.5 km, only waves with periods longer than 20 seconds will create a detectable seafloor signal. These waves are known as infragravity waves.
Compliance is measured at low frequencys (between ~0.002 and 0.1 Hz), where the pressure signal comes from linear ocean surface gravity waves known as infragravity waves.
The wavelengths and frequencies are related by the dispersion equation \begin{equation} \omega ^2 = g k \tanh (k _w H) , \label{eqn:dispersion} \end{equation} where $g$ is the local gravitational acceleration, $H$ is the water depth, and $k = 2 \pi / \lambda _w$ is the ocean surface wavenumber [{\it e.g., Gill}, 1982, p.102]. The pressure signal amplitude at the seafloor is \begin{equation} P_{sf}(\omega ) = \rho _w g h_w (\omega ) / \cosh (k (\omega) H) , \label{eqn:depthdecay} \end{equation} where $\rho _w$ is the density of water and $h_w (\omega )$ is the sea surface displacement. The $ \cosh (k (\omega) H)$ term strongly attenuates short wavelengths, so that the waves generate significant seafloor pressure fluctuations only for ocean surface wavelengths greater than the water depth.