Ramanujan's tau function
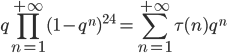
It looks simple, isn't it ?
But computation of τ(n) is not ...
First values are:
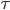 (1)
= 1
(1)
= 1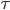 (2)
= -24
(2)
= -24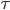 (3)
= 252
(3)
= 252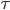 (4)
= -1472
(4)
= -1472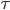 (5)
= 4830
(5)
= 4830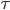 (6)
= -6048
(6)
= -6048Ramanujan found it has remarkable properties:
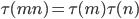 for m, n coprime integers,
for m, n coprime integers,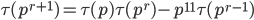 for p prime.
for p prime.Now we need a formula to compute τ(p) for all primes p.
A formula related to Catalan triangle
From Eichler-Selberg trace formula, one may derive
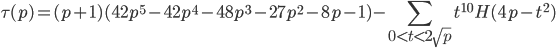
where p is prime, and H(n) is Hurwitz-Kronecker class number of binary quadratic forms of negative discriminant -n.
A new and faster formula
Recombining several traces leads to the formula
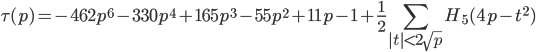
where p is prime and H5(n)=n5H(n).
Note that it mainly consists of a finite sum in the table of H5(n) integers. Hence it is a somewhat faster algorithm when computing τ(p) for all primes.
After rearrangement, I obtained the nice formulation
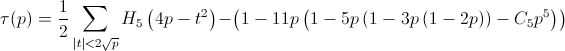
where C5 = 42 is the 5th Catalan number.
Non-ordinary primes
We found that the only primes p for which τ(p) ≡ 0 (mod p) are 2, 3, 5, 7, 2411 and 7758337633, up to 1010.
See OEIS entry: A007659
Odd prime values
Our purpose is to identify the integers n for which τ(n) is an odd prime, disregarding the sign of τ(n). The main result is the following :
Theorem
Let n be a positive integer such that τ(n) is an odd prime. Then n is of the form pq-1 where p and q are odd primes and p is ordinary.
One sets LR(p, q) := τ(pq-1), where "LR" stands for Lehmer-Ramanujan.
Here we give all known pairs (p,q), p < 100, such that LR(p, q) is prime (P) or probable prime (PRP):
| (p, q) |
Digits* |
Primality |
Verified by |
Software |
End date |
Duration |
| (11, 317) |
1810 |
P |
Olivier Rozier |
PARI/GP |
||
| (17, 433) |
2924 |
P |
Olivier Rozier |
PARI/GP |
12/02/2011 |
10 hrs |
| (29, 31) |
242 |
P |
||||
| (29, 83) |
660 |
P |
||||
| (29, 229) |
1834 |
P |
Olivier Rozier |
PARI/GP |
||
| (41, 2297) |
20367 |
P |
François Morain |
ECPP |
06/04/2018 |
24 days |
| (41, 28289) | 250924 | PRP |
||||
| (47, 5) |
37 |
P |
||||
| (47, 47) |
424 |
P |
||||
| (47, 4177) |
38404 |
P |
Andreas Enge |
CM/ECPP |
22/06/2022 |
15 days |
| (59, 1381) |
13441 |
P |
Gerasimos Politis** |
Primo |
12/10/2013 |
83 days |
| (59, 8971) |
87365 |
PRP |
||||
| (79, 1571) |
16386 |
P |
Gerasimos Politis** |
Primo |
07/02/2014 |
|
| (79, 6317) |
65920 |
PRP |
||||
| (89, 73) |
772 |
P |
||||
| (97, 331) |
3606 |
P |
Olivier Rozier |
PARI/GP |
16/02/2011 |
31 hrs |
| (97, 887) |
9682 |
P |
Keira Stambolidou** |
Primo |
26/05/2013 |
(*) number of decimal digits of LR(p, q)
(**) supervised by Nik Lygeros and Olivier Rozier
and the distribution of such values, for p < 1000, on a semi-log scale :
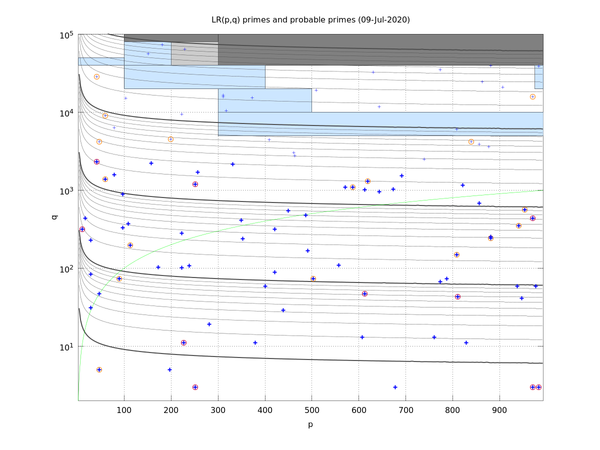
LR_data.pdf : known (probable) prime values LR(p,q) with p<1000
Numerical data
Tau_0001000000.zip (1.4 Mb): tau(p) for all primes p < 10^6
Tau_0010000000.zip (13.4 Mb): tau(p) for all primes p < 10^7
Publications
N. Lygeros & O. Rozier, Odd prime values of the Ramanujan tau function, Ramanujan Journal, 10.1007/s11139-012-9420-8 (2013)
N. Lygeros & O. Rozier, A new solution to the equation τ(p) ≡ 0 (mod p), Journal of Integer Sequences 13, article 10.7.4 (2010)
home page
Ramanujan's tau function © 2010 Olivier Rozier
