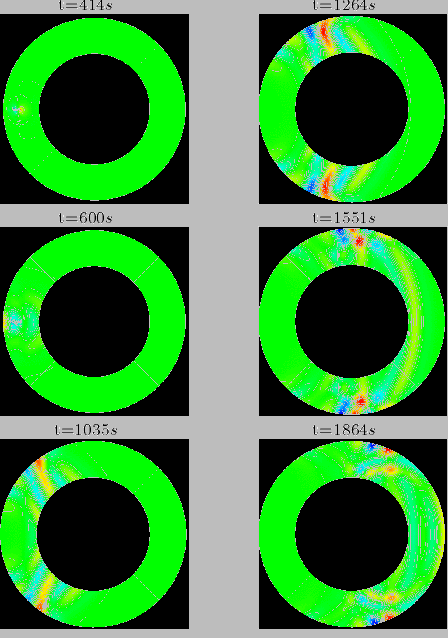
Propagation du champ d'onde dans un sphère elastique homogène sans rotation. La source est explosive. La fonction source est une ondelette en temps de période centrale 312 secondes. La source est localisée à une profondeur de 1048 Km.
Dans la coque sphérique externe, on résoud une formulation variationnelle de l'équation de l'élastodynamique. La méthode repose sur une discrétisation en espace par la méthode des éléments spectraux, et une discrétisation en temps par un schéma de type Newmark explicite du second ordre. La coque sphérique est discrétisée via la transformation de la sphère cubique. Chacune des six régions de la sphère comporte 8 × 8 × 2 élements, avec une degré polynomial de 8. Dans la sphère interne, en noir sur les figures, l'équation de l'élastodynamique est résolue dans le domaine fréquence-nombre d'onde par une méthode de sommation de modes normaux. En espace, on utilise une représentation sur la base des harmoniques sphériques généralisées avec l_max = 47. Les deux méthodes sous couplées via un opérateur DtN régularisé en espace et en temps. L'interface de couplage est localisée à 3471 Km.
Les figures représente des instantannés du déplacement dans une coupe méridienne. Le champ de déplacement est représenté en espace et en temps uniquement dans le domaine des éléments spectraux. On observe sur les figures, au cours du temps :

• Au temps t = 600 secondes, l'onde P qui pénètre dans le domaine interne de la méthode de sommation de modes. Il n'y a aucune réflection visible attestant de la qualité de la méthode de couplage.
• Au temps t = 1035 secondes, l'onde pP, onde P réfléchie à la surface, est à son tour absorbée par l'opérateur DtN et transmise dans la sphère interne.
• au temps t = 1551 secondes, on observe la transmission de l'onde P depuis la sphère interne dans la coque externe des éléments spectraux. Il n'y a aucun déphasage visible.
• On notera en surface, l'onde de Rayleigh, associée au premier mode de vibration sphéroïdal. Cette onde n'est pas dispersive. La deuxième `` onde de surface '' visible est la phase X qui correspond à une succession de réflections sous la surface et de conversions entre les ondes P et S. En termes de modes, cette phase correspond à une surperposition d'harmoniques sphéroïdaux. En raison de la position de la source, la pahse X est ici très excitée alors que la Rayleigh est faible.