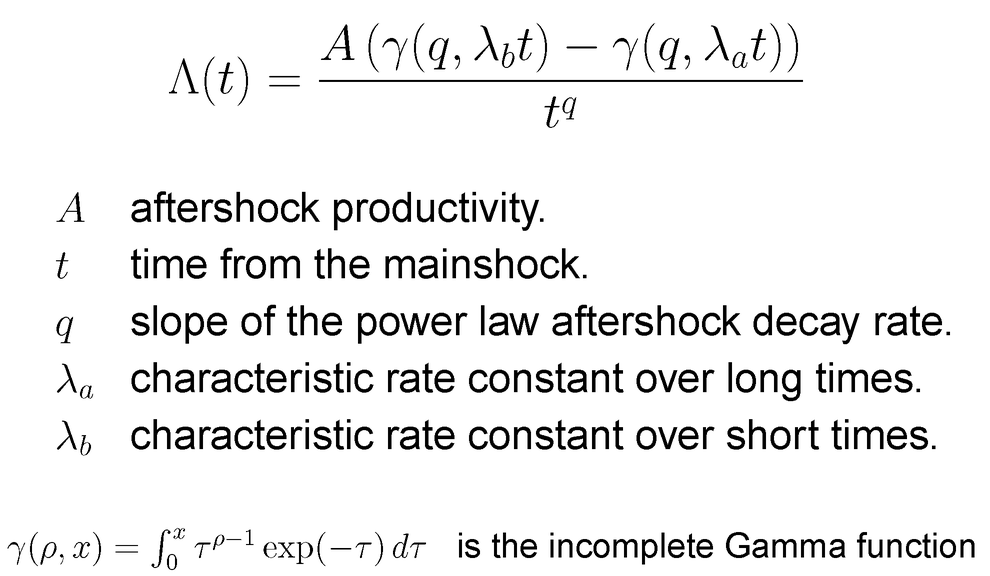Aftershock Sequences
After a large event, the so-called main shock, aftershocks are smaller earthquakes resulting of
perturbations of the state of stress.
In a Limited Power Law model, the aftershock rate results from the
superposition of independent exponential decay rates with different
characteristic time constants: these characteristic times to failure
represent the time-dependent strength of the different seismogenic
domains within the aftershock zone according to a mechanism of static
fatigue.
You can derive the Modified Omori law from the Limited Power Law
(see the comparison here).
In the Limited Power Law model, the power-law aftershock decay rate
is limited in time by two
characteristic rate constants (see Narteau et al., 2002):
Over short times, a linear
decay rate dominates:
Considering that aftershocks result from a steplike perturbation of
stress in the neighbourhood of a triggering event, the model predicts
that the amplitude of this perturbation controls the duration of the
linear regime of the aftershock decay rate over short time.
We use
this time delay before the onset of the power-law aftershock decay rate
to estimate variation of the differential shear stress in active
tectonic settings (see Narteau
et al., 2005, Narteau et
al., 2008 and Narteau et
al., 2009).
Over long times, an
exponential decay rate dominates:
Under low stress these strengthening processes may dominate, and
prevent rupture initiation. For small stress, we adopt a different
time-depedent behavior by considering a fracturing threshold. Below
this threshold, the time required to produce an aftershock becomes
infinite. This may be described as a minimum velocity of subcritical
crack growth. As a result, the power-law aftershock decay rate is
remplaced by an exponential decay over long times (see Narteau et al., 2003).
_______________
A limited power-law model
for the aftershock decay rate
_______________