Despite considerable improvements of
the knowledge of the earthquake machine in various scientific
disciplines (tectonics, seismology, rock physics, etc..), a
complete understanding of seismic sequences and their prediction are
still out of reach.
In the upper seismogenic crust, self-similar faulting and seismic patterns are observed worldwide across many different types of geological environments. Classical examples of power-law relationships include fracture-length distributions, aftershock decay rates and the well-known Gutenberg-Richter law between the magnitude of an earthquake and its characteristic recurrence time. Historically, self-organized criticality states observed in sand-pile and slider block models have been used as a paradigm for the earthquake-size distribution. These models serve as an analogy for coseismic rupture propagation by illustrating how short-range interactions and a random element can result in an instability that can spread across the entire system. These precursory works have also demonstrate that a cellular automaton approach can be a useful complementary tool for the modelling of earthquake dynamics. In our work, we analyse the feedback mechanisms, positive or negative, that can be involved in the brittle deformation processes of the brittle upper crust (earthquake triggering, fault interactions, fluid-rock interactions, aseismic transients). We develop discrete numerical codes for the modelling of earthquake and faulting patterns. This new generation of models combine long-range interactions that mimics the continuum elastic solutions while retaining the inherently discrete approach of statistical physics. In addition, we analyse the earthquake phenomenology with a special interest on aftershock sequences. See applications on |
 The San-Andreas fault at Carrizo Plain
|
Earthquake and Faulting patterns in California
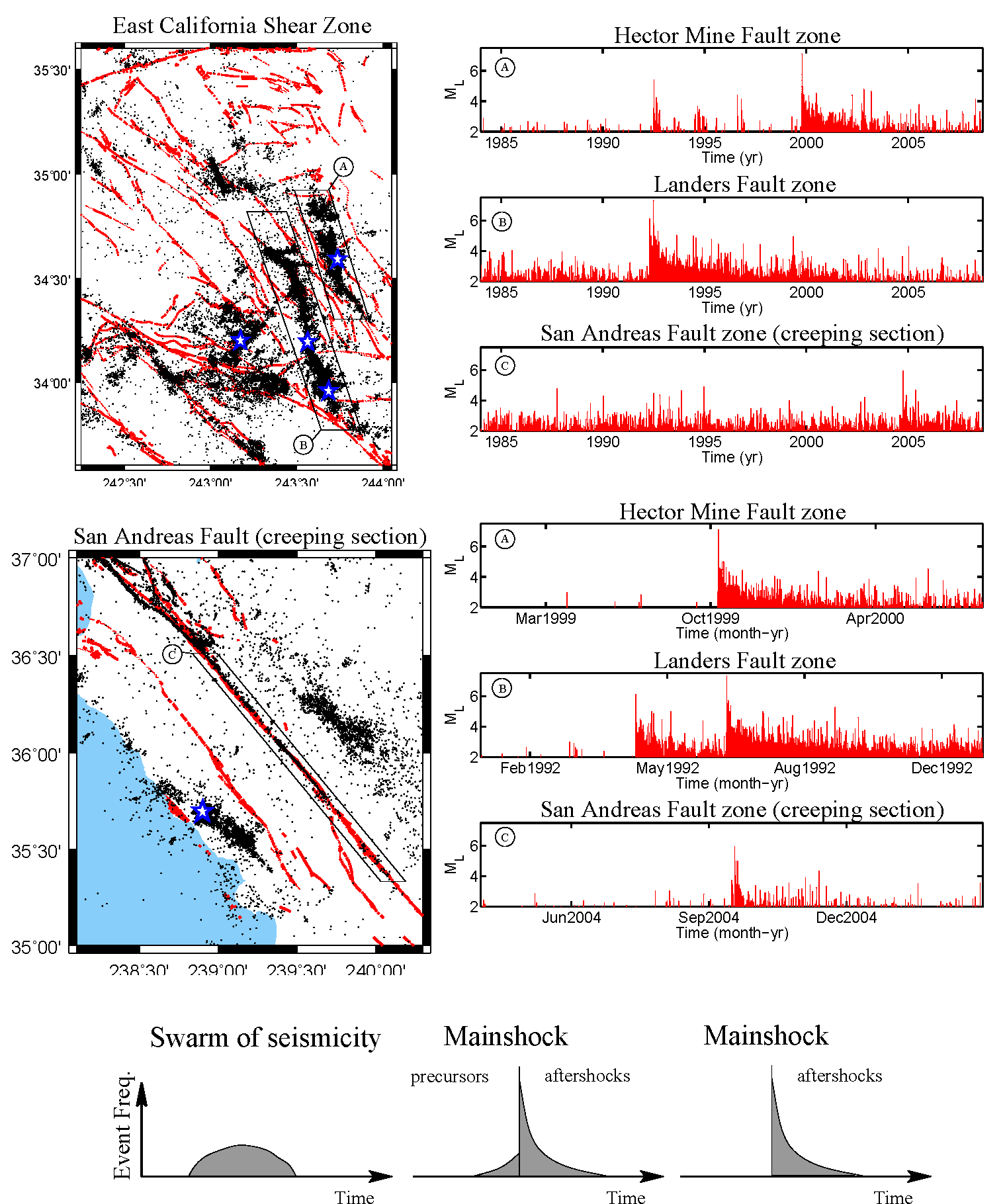
Different types of seismic sequences