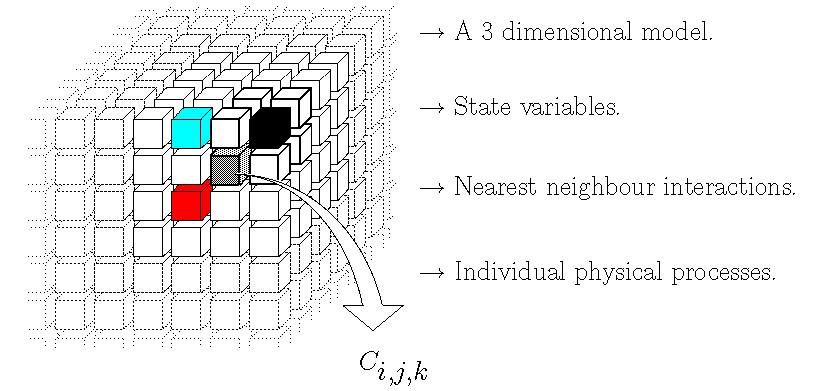
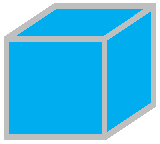
Real-Space Cellular Automaton Models

In a vast majority of cases, a numerical model is a set of physical variables (temperature, pressure, velocity, etc...) that are recalculated over time according to some predetermined rules or equations. Then, any point in space is entirely characterized by a local set of parameters. This is not the case in Real-Space Cellular Automaton Models where the only local variable is a state-parameter that represent the different phases involved in the problem.








\







              

 




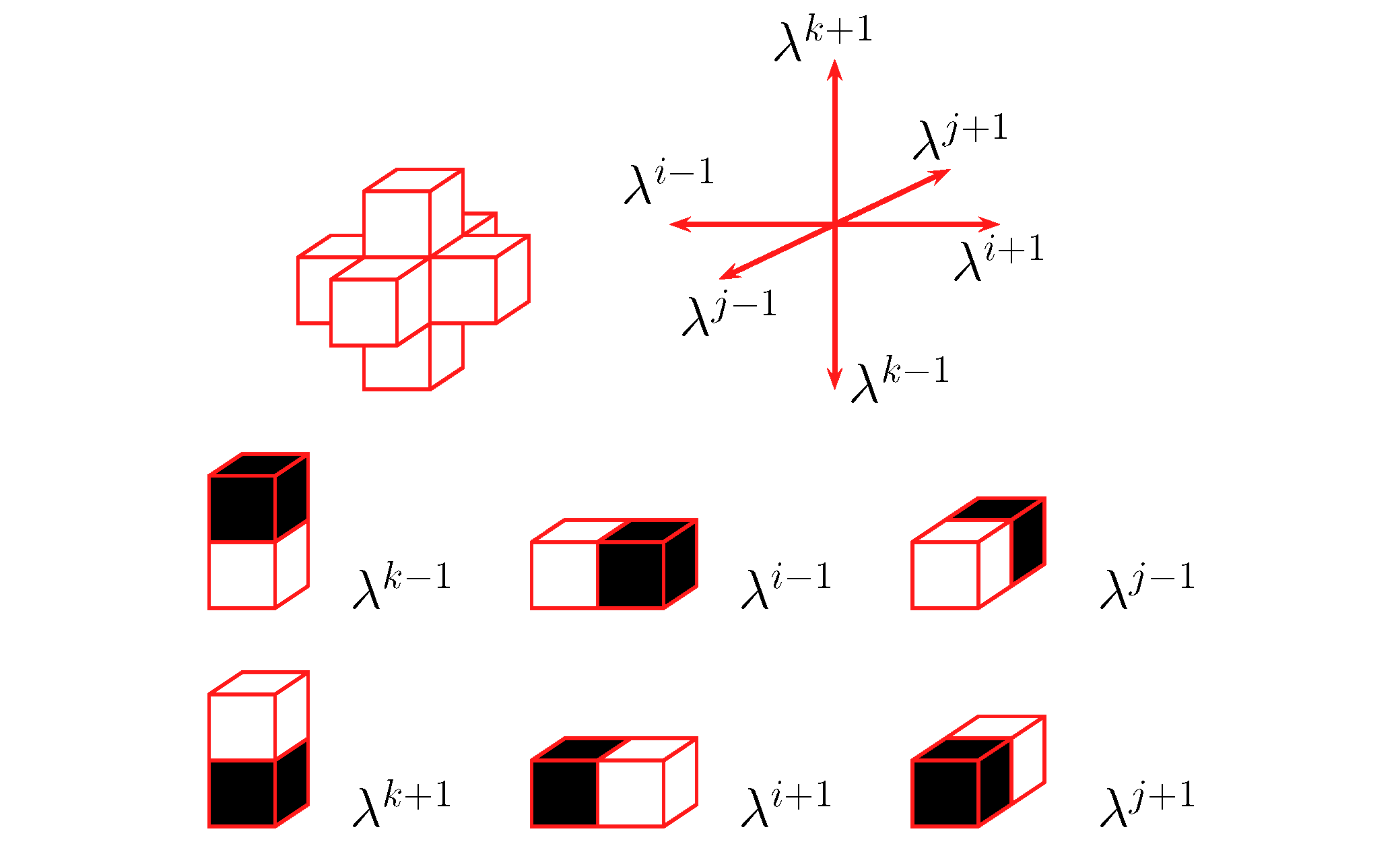
An elementary cell is a cube of edge length l0 and pairs of nearest neighbour cells are called `doublet'. For each individual physical process that we take into account, there is a set of doublet transitions.

Each transition is associated with a rate parameter with units of frequency  that introduces into the model the characteristic time scale of the corresponding physical mechanism. Doublets are all supposed to be independent and the occurrence of a transition of doublet is assumed to follow a stochastic process.

    

 


Using this approach we can model a wide range of physical-chemical or anthropological processes.

See applications in geosciences in Narteau et al. (2001) and Narteau et al. (2009) .



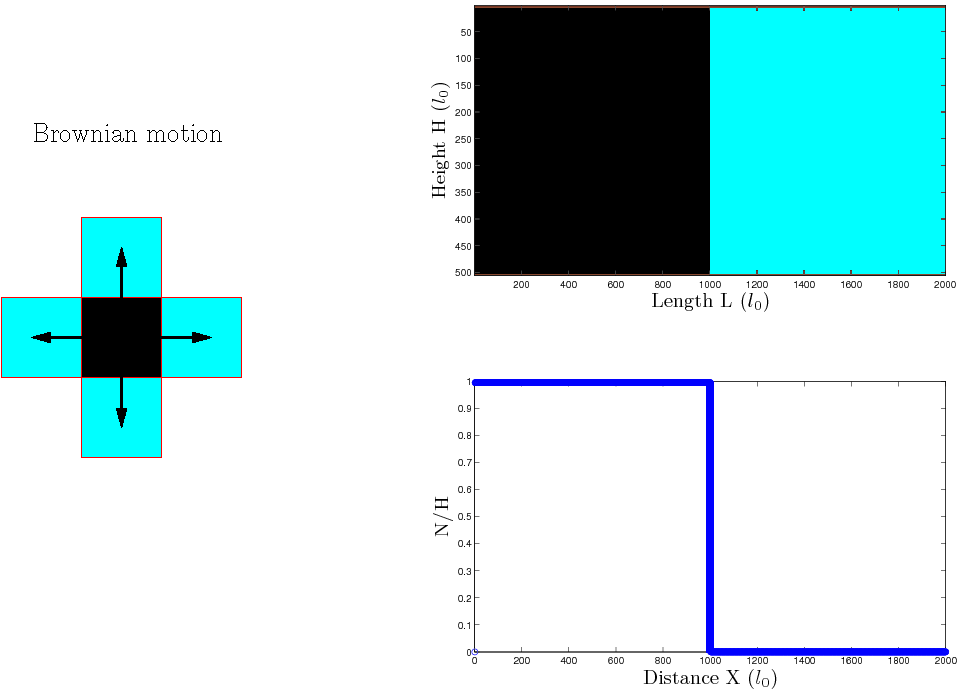
For example, we can study molecular diffusion in 2-D, with 2 states (Air = ; Molecule =  ) and four transitions for the random motions particules (see the animation):