From left to right: density anomaly field, azimuthal velocity and radial magnetic field renderings inside a high-resolution geodynamo simulation (see Aubert 2019)
From left to right: density anomaly field, azimuthal velocity and radial magnetic field renderings inside a high-resolution geodynamo simulation (see Aubert 2019)
Simulating the geodynamo in a computer is a stiff problem that has been investigated since a few decades. The first self-consistent, three-dimensional simulations of the geodynamo have been obtained in the mid 1990’s. The success of these early models was striking, given their modest spatial and temporal resolution. Questions have rapidly arisen whether we were getting “the right answers for the wrong reasons” i.e. obtaining Earth-like output in a wrong physical regime. Today we know that this was not the case, as the numerical models can be connected to the Earth’s core conditions through a ‘parameter space path’ along which the main details of the dynamical force balance are preserved.
Today we simulate the geodynamo on French supercomputers and our regional mesocentre.
Fully simulating the very fine turbulence sustaining the geomagnetic field over long temporal ranges relevant to the geodynamic evolution of the Earth is out of reach of the present supercomputers, and will in fact always be. But using the ‘path’ theory as well as relevant approximations, we can either simulate the fine-grained details of this turbulence over short times (see images above) and with high temporal resolution or a more coarse, large-scale system over long periods of time with lower temporal resolution. We obtain a hierarchy of models which, put together, strengthen our understanding of the geodynamo, including explanations for its notable features such as the geomagnetic westward drift.
Radial magnetic field at the core-mantle boundary (milliteslas) from a ‘coarse’ model, reproducing the geomagnetic westward drift (from Aubert et al. 2013)
azimuthal flow acceleration at the core-mantle boundary (km per year squared) in a fine-grained simulation during a geomagnetic jerk
Numerical geodynamo simulations are also investigated through scaling analyses aiming at extracting the power-law dependences with control parameter of the main simulation outputs. Scaling theories have also been elaborated to explain these power laws. Scaling can also be used to elaborate a history of the geodynamo from the variation of the power of the cooling through geological time. With the availability of the ‘path’ theory, scaling has become more precise than before as power laws along the parameter space path can be derived with a greater accuracy.
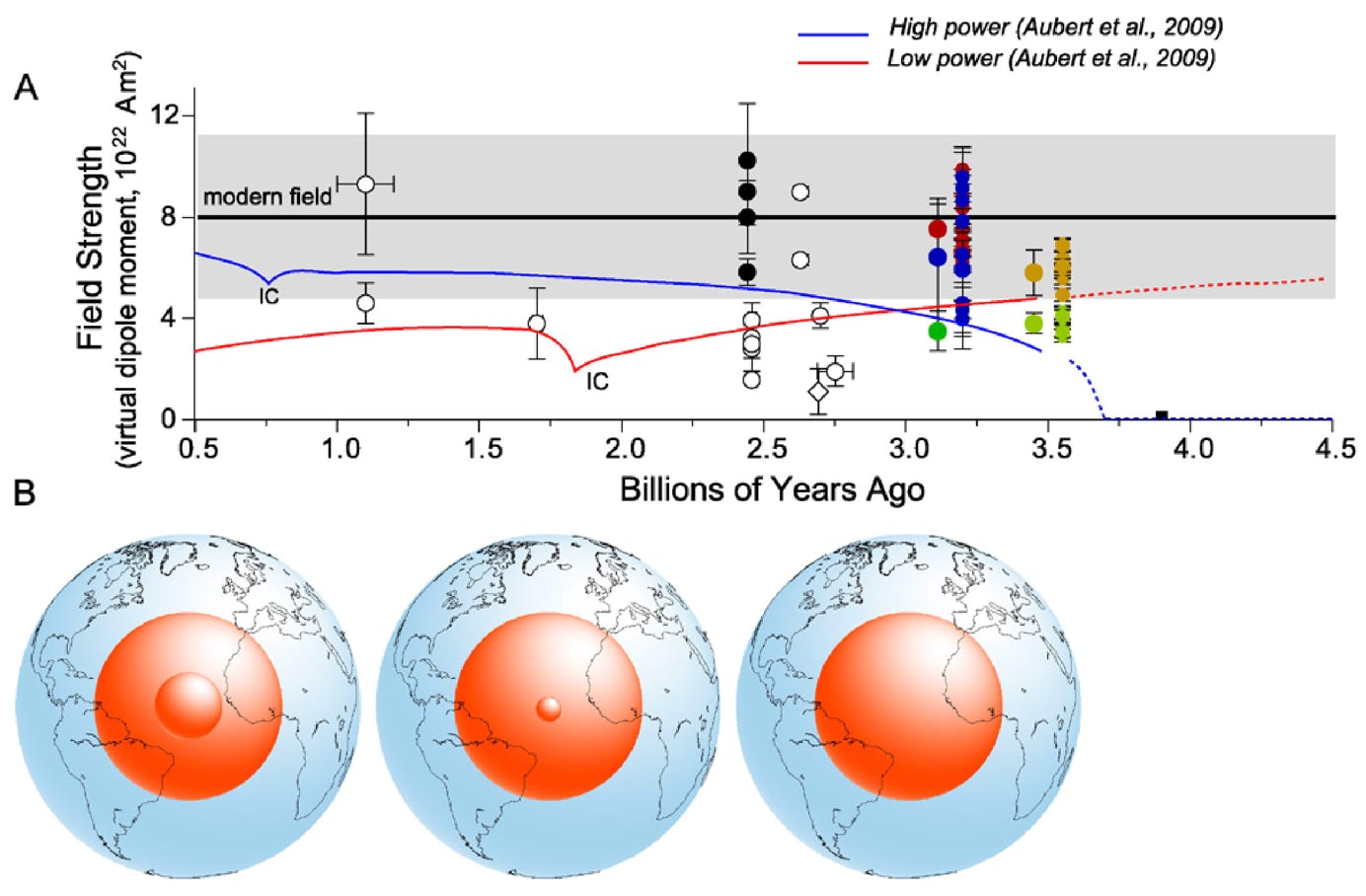
several paleo-evolution scenarii for the geodynamo derived from scaling analyses, compared with paleomagnetic intensity data (from Aubert, Johnson, Tarduno, 2010)
Aubert, J.: Approaching Earth’s core conditions in high resolution geodynamo simulations, Geophysical Journal International 219 S1, S137-S151, 2019, doi: 10.1093/gji/ggz232.
Aubert, J. and Finlay, C.C.: Geomagnetic jerks and rapid hydromagnetic waves focusing at Earth’s core surface, Nature Geoscience 12, 393-398, 2019, doi: 10.1038/s41561-019-0355-1
Aubert, J., Gastine, T., and Fournier, A.: Spherical convective dynamos in the rapidly rotating asymptotic regime, J. Fluid. Mech. 813, 558-593, 2017, doi: 10.1017/jfm.2016.789
Aubert, J., Finlay, C., Fournier, F.: Bottom-up control of geomagnetic secular variation by the Earth’s inner core, Nature 502, 219-223, 2013, doi: 10.1038/nature12574
Christensen, Aubert, Hulot: Conditions for Earth-like geodynamo models, Earth. Plan. Sci. Lett. 296, 487-496, 2010, doi:10.1016/j.epsl.2010.06.009
Christensen, Aubert: Scaling properties of convection-driven dynamos in rotating spherical shells and application to planetary magnetic fields, Geophys. J. Int. 166, 97-114, 2006, doi: 10.1111/j.1365-246X.2006.03009.x